The Neuro-Symbolic Divide
Can We "Un-Smear" the Black Box?
Artificial Intelligence is currently fractured between two powerful but incompatible paradigms.
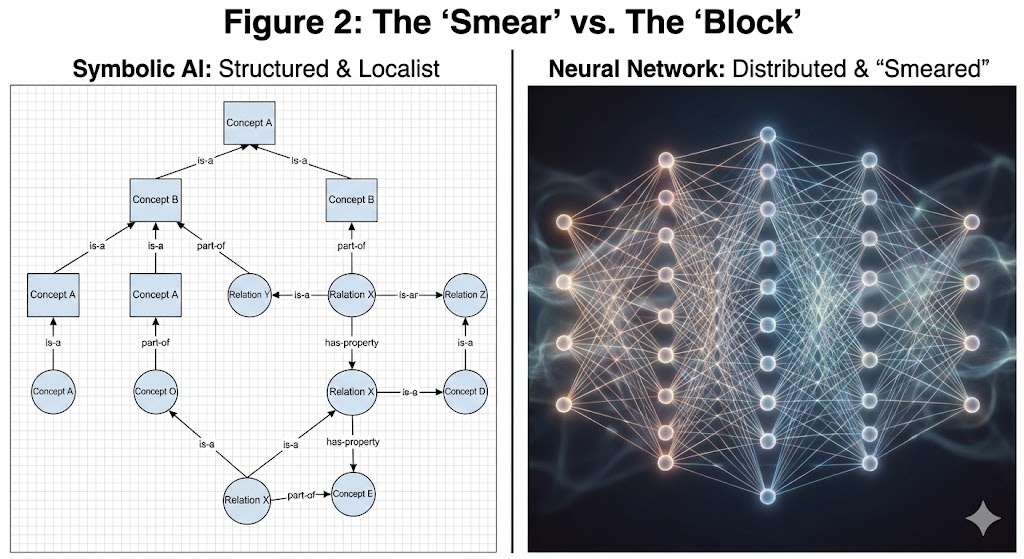
On one side, we have Symbolic AI . It is defined by clarity and structure. It relies on localist representations—ontologies and knowledge graphs—where every node has a distinct address and meaning. It is perfectly interpretable, extends infinitely, and suffers no context limits. However, it has a fatal flaw: brittleness. It shatters when faced with the noise and ambiguity of the physical world.
On the other side, we have Neural Networks . These are masters of noise, thriving on the messy, distributed patterns of reality. But they are opaque black boxes. Their knowledge is "smeared" across millions of weights in a holographic fog—a phenomenon recently characterized as superposition (Elhage et al., 2022) . Because concepts are entangled, we cannot easily peek inside to see what the network knows, nor can we add to it safely. When we attempt to teach a trained network a new fact, the necessary weight updates inevitably disrupt existing patterns, leading to Catastrophic Forgetting (McCloskey & Cohen, 1989) .
The Question: Is there a way to combine the infinite, safe extensibility of an Ontology with the noise-tolerance of a Neural Network?
The Hypothesis:
If we use a strict Ontology as a curriculum, can we force a Neural Network to organize itself into discrete, interpretable "blocks" instead of a distributed mess?
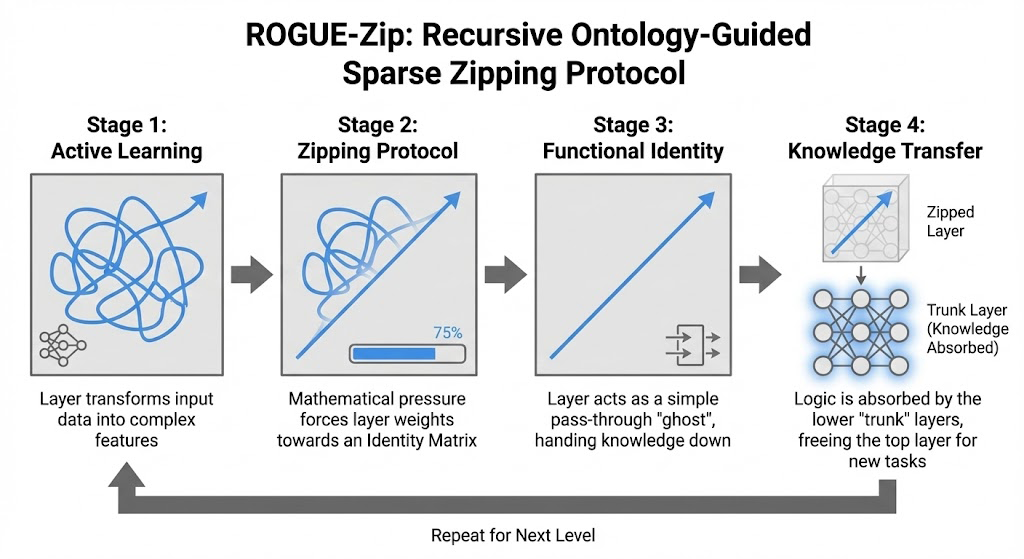
To answer this, I developed a novel training protocol called Recursive Ontology-Guided Sparse Zipping (ROGUE-Zip) .
The goal of ROGUE-Zip is ambitious: Train a network layer to learn a specific level of an ontology, and then mathematically force that layer to "hand over" the knowledge to the layers below it, resetting itself to a clean Identity Matrix. By combining this with sparsity constraints, we aim to physically sequester knowledge deep in the network—building a neural brain that grows layer by layer, concept by concept, without forgetting what it learned before.
The Apparatus & Implementation
Building a "Transparent Box" for Neural Research
To validate the ROGUE-Zip architecture, we first needed to prove the fundamental physics of the "Zip"—the ability to transfer logic between layers without loss. This required a custom tooling approach, eschewing standard black-box libraries for a pixel-perfect visualization of the network's internal state.
1. Biological Inspiration: Systems Consolidation
Our architecture is not arbitrary; it mimics the mammalian solution to the stability-plasticity dilemma. As established by McClelland et al. (1995) , the brain utilizes a complementary learning system: rapid acquisition of fragile memories in the Hippocampus , followed by a period of "sleep" (systems consolidation) where those memories are interleaved into the Neocortex for permanent storage.
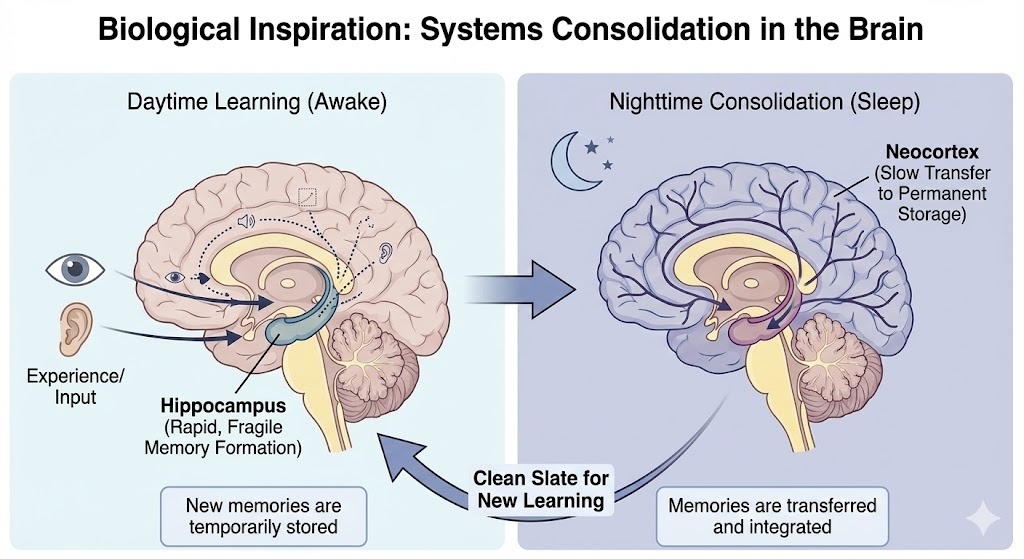
Standard Neural Networks lack this "Sleep" phase. They are "always awake," meaning every new gradient update impacts the same shared weights as the previous tasks. ROGUE-Zip attempts to engineer a synthetic version of this consolidation cycle, treating the top layer as the Hippocampus (Short-Term Memory) and the lower layers as the Neocortex (Long-Term Instinct).
2. The Mechanism: The Identity Matrix
To implement this consolidation mathematically, we utilize a specific linear algebra concept: the Identity Matrix .
In a neural network, if a layer’s weights form an Identity Matrix (a perfect diagonal line of 1s, with 0s everywhere else), that layer becomes a "ghost." It passes data through unchanged ($f(x) = x$), effectively contributing zero cognitive work to the system.
While Chen et al. (2015) famously used identity initializations to expand network capacity (the "Net2Net" approach), ROGUE-Zip inverts this paradigm. We use asymptotic identity constraints to compress active logic into lower layers, recycling the layer for future tasks.
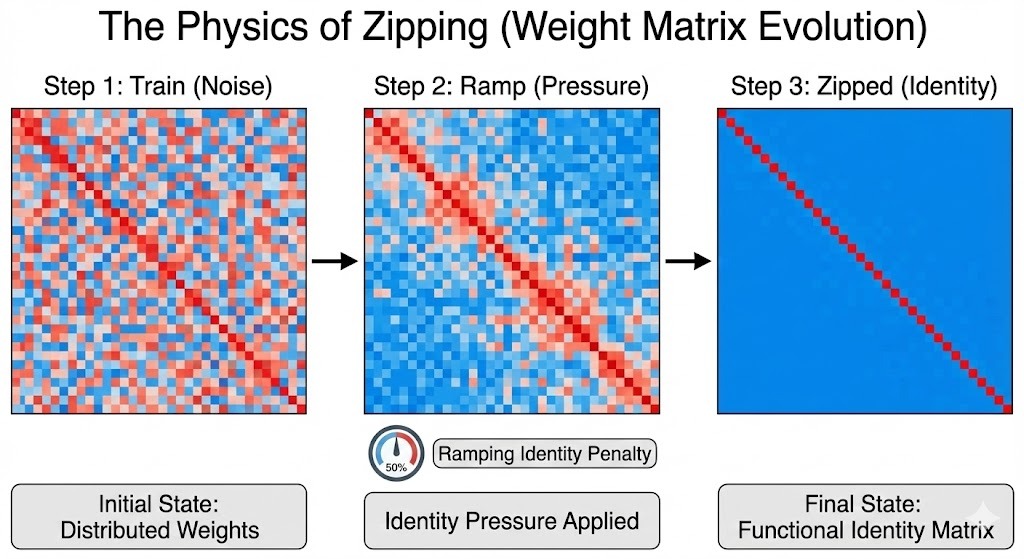
3. The Physics of Zipping: A Multi-Objective Tug-of-War
The core engineering challenge was creating a training loop that respects two contradictory goals simultaneously. We rejected the standard "Head Switching" approach in favor of a Gradient Superposition strategy.
$$\nabla_{Total} = \nabla_{Distillation} + \lambda(t) \cdot \nabla_{Identity}$$
By slowly ramping the identity pressure ($\lambda$) over thousands of epochs, we create a "Tug-of-War." The layer is forced to straighten out, but the accuracy gradient acts as a tether, ensuring it only straightens as fast as the lower layers (The Trunk) can absorb the logic.
4. Critical Design Decision: The Topological Valve
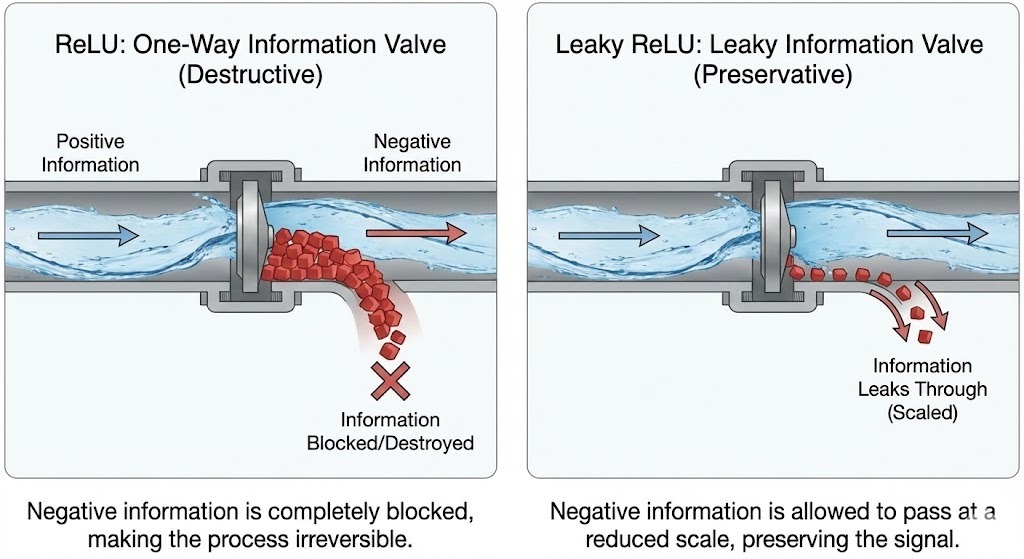
During early testing, we encountered a theoretical roadblock that caused total collapse. We discovered that the choice of activation function is critical for Zipping.
- The Failure (Standard ReLU): As a layer approaches Identity, it passes raw features forward. If those features are negative, ReLU deletes them ($max(0, -x) = 0$). This renders the transformation non-invertible —the Trunk cannot "pre-compensate" for deleted data.
- The Fix (Leaky ReLU): We switched to a Leaky ReLU. This ensures that even as the layer becomes a "ghost" (Identity), the information pipeline remains open (bijective). Negative values are scaled, not destroyed, allowing the lower layers to adapt.
5. The Interactive Notebook
This is not a static paper; it is a live experiment. To allow for reproducibility and exploration, I built
The HCL Trainer v8
—a custom, "transparent-box" neural network engine in vanilla JavaScript. It visualizes every weight matrix and activation vector in real-time, allowing us to visually verify that the "Zipping" process is structurally valid and not just a statistical illusion.
Try the Interactive HCL Trainer v8
here
.
We invite you to use this apparatus to replicate the experiments below, specifically contrasting the successful "General-to-Specific" curriculum against the failed "Physical-to-Abstract" curriculum.
Experimental Results
The "House of Cards" vs. The "Strong Foundation"
With the apparatus calibrated and the Handover Protocol stabilized, we executed two distinct curriculum experiments to test the limits of the ROGUE-Zip architecture. The results provided a stark contrast between Residual Learning (Success) and Catastrophic Forgetting (Failure), offering critical insights into how neural networks organize hierarchical knowledge.
Experiment A: The Success (L2 $\to$ L3)
The Curriculum: "General-to-Specific"
- Foundation: Train on L2 Categories (e.g., Mammal vs. Vehicle).
- Zip: Handover logic to Trunk. (Block 4 $\to$ Identity).
- Extension: Train on L3 Subgroups (e.g., Dog vs. Car).
The Observation:
As we began training on L3, the "Zip" (Identity Matrix) in Block 4 naturally dissolved. The "OffDiag" score rose rapidly, indicating the layer was mutating to handle the new complexity.
However, the L2 Accuracy (Green Line) remained high (~90%) throughout the entire process.
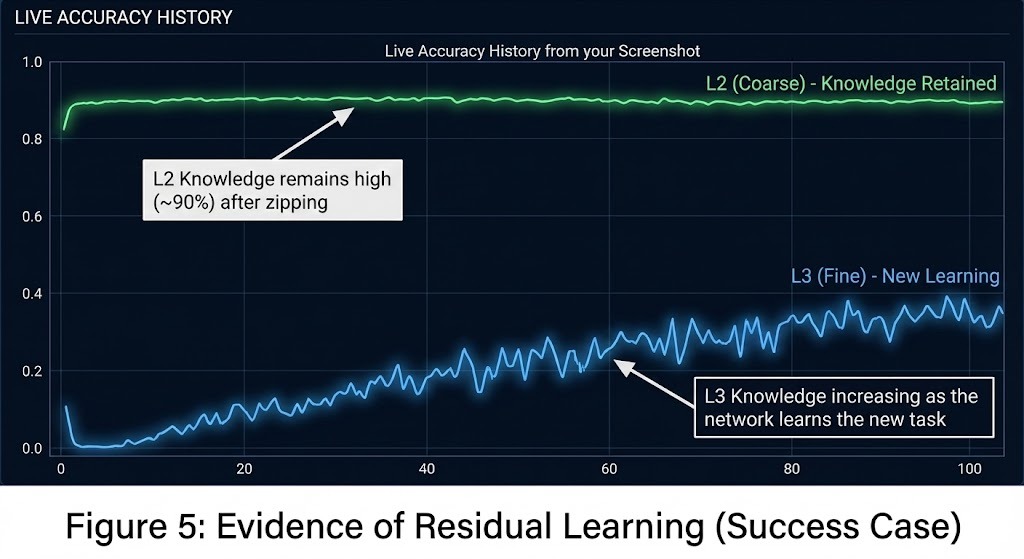
This is a textbook demonstration of Residual Learning. By Zipping L2, we forced the "Trunk" (Blocks 1-3) to become a robust, general-purpose feature extractor. When we asked the network to learn L3, it did not need to rewrite the Trunk; it simply utilized the existing "Mammal" features and added a fine-tuning layer in Block 4 to distinguish "Dog" from "Cat." The foundation held.
Experiment B: The Failure (L1 $\to$ L2)
The Curriculum: "Physical-to-Abstract"
- Foundation: Train on L1 Motion (Moving vs. Static).
- Zip: Handover logic to Trunk.
- Extension: Train on L2 Categories (Mammal vs. Vehicle).
The Observation:
The moment we applied pressure to learn L2, the system collapsed. The accuracy for the previous task (L1) plummeted, and the network struggled to learn the new task. It was a complete House of Cards collapse.
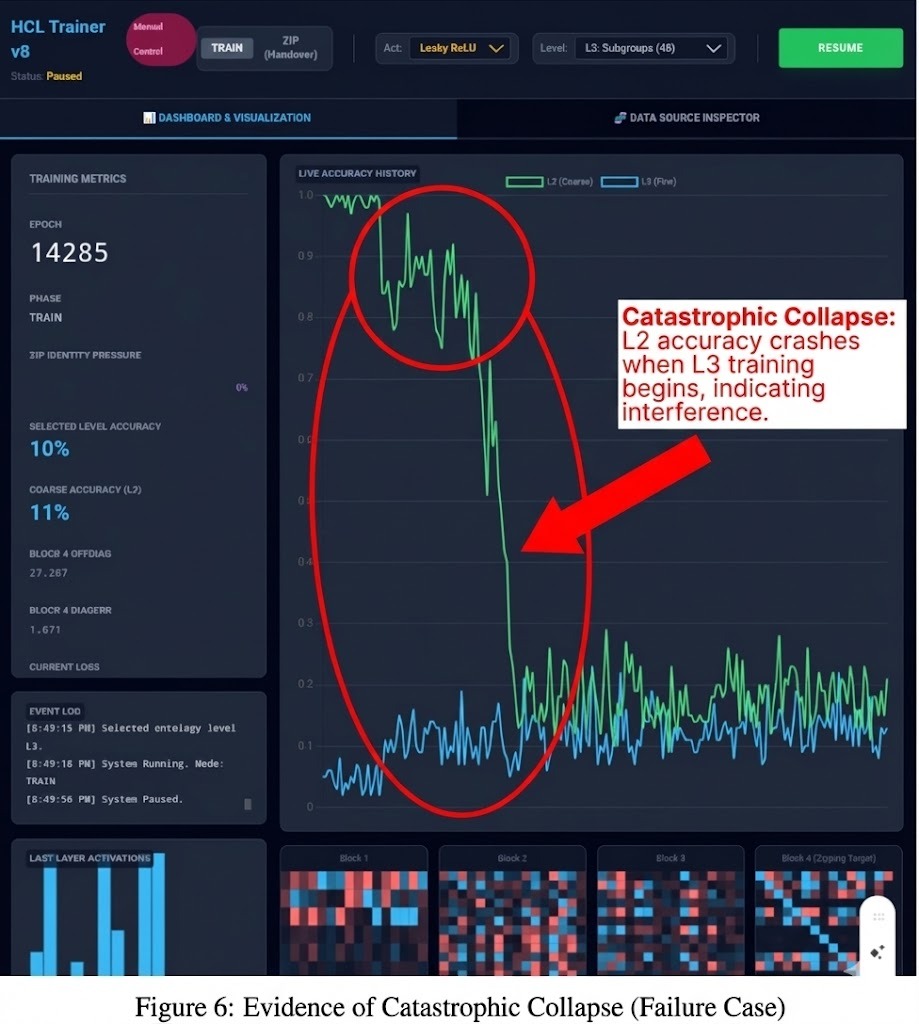
The Interpretation: The "Gerrymandering" Problem
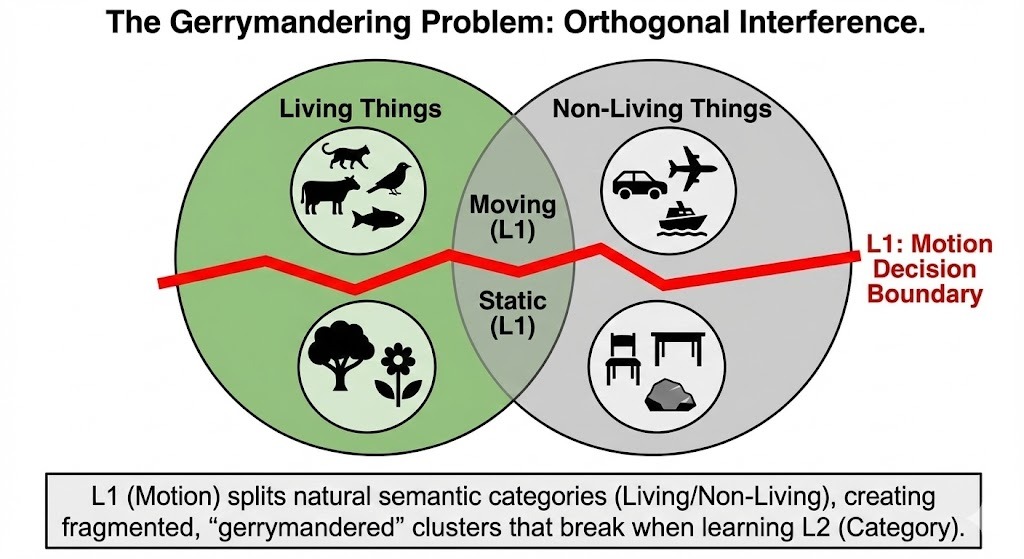
This failure mirrors the classic Catastrophic Interference phenomenon described by McCloskey & Cohen (1989), but with a specific topological cause. We hypothesize that L1 (Motion) creates Orthogonal Decision Boundaries relative to L2 (Category).
- "Living Things" contains both Moving entities (Mammals) and Static entities (Plants).
- "Non-Living Things" contains both Moving entities (Vehicles) and Static entities (Furniture).
By forcing the Trunk to lock into a "Motion-based" worldview first, we essentially gerrymandered the neural representation. When we later asked it to group "Mammals" and "Plants" together (as Living things), the network had to shatter its existing Motion boundaries to comply. The foundation wasn't just insufficient; it was actively fighting the new structure.
Key Finding: Curriculum Matters
The ROGUE-Zip protocol is powerful, but it obeys the principles of Curriculum Learning (Bengio et al., 2009) . These experiments suggest a fundamental rule for Neuro-Symbolic training: The Foundation must be Semantic, not just Statistical.
A "General" foundation (like Categories) creates a trunk that can support specific details. A "Narrow" foundation (like Motion) creates a rigid trunk that shatters when the worldview expands. Zipping works best when we follow the natural hierarchy of the ontology, moving from broad, inclusive concepts down to specific differentiations.
Technical Deep Dive
The Physics of Forcing Identity
While the concept of ROGUE-Zip is intuitive—"make the layer a ghost"—the mathematical implementation is violent. Forcing a non-linear, high-dimensional transformation to collapse into a linear Identity Matrix fights against the natural gradient descent process.
Here is the post-mortem of the technical hurdles we cleared to make the Handover Protocol stable.
1. The Optimization Problem: Orthogonal Gradient Decoupling
In our initial attempts (v4-v5), we tried a "Hard Zip" approach where we manually overwrote the gradients of Block 4:
block4.W.grad.fill(0)
We assumed we could freeze the "Accuracy" optimization and purely optimize for "Identity." This failed because it decoupled the parameters $\theta_4$ from the global loss function. The optimizer marched blindly toward the Identity Matrix $I$, moving orthogonal to the complex manifold required to maintain feature coherence. The result was immediate representational collapse.
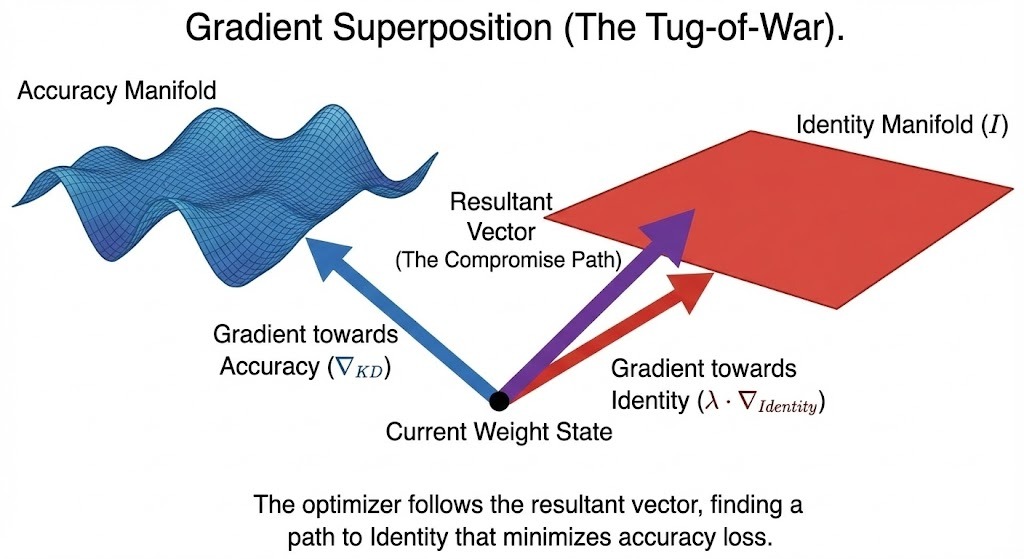
The Fix: Gradient Superposition
We moved to a multi-objective optimization strategy. We retained the backpropagated gradients from the distillation loss ($\mathcal{L}_{KD}$) and added the identity penalty gradients:
$$\nabla_{\theta_4} \mathcal{L}_{Total} = \nabla_{\theta_4} \mathcal{L}_{KD} + \lambda(t) \nabla_{\theta_4} \mathcal{L}_{Identity}$$
This turns the process into a dynamic equilibrium. The optimizer finds a path to $I$ that lies within (or very close to) the null space of the accuracy loss, effectively rotating the "Trunk" to compensate for the stiffening of Block 4.
2. The Topological Failure: Non-Injective Mapping
Standard neural networks rely on ReLU ($\sigma(x) = \max(0, x)$).
In the limit where $W_4 \to I$ and $b_4 \to 0$, the function of Block 4 becomes simply $f(x) = \text{ReLU}(x)$.
This transformation is non-injective (not one-to-one). Any feature vector $x$ containing negative components—which often encode critical ontological contrasts—is mapped to $0$. This constitutes an irreversible destruction of information entropy. The Trunk layers ($W_{1-3}$) cannot "pre-compensate" for this because they cannot encode information in the negative domain that survives a pass-through Identity-ReLU block.
The Fix: Bijectivity via Leaky ReLU
We switched to Leaky ReLU ($\alpha = 0.01$). This restores the bijectivity of the transformation. Even as $W_4 \to I$, the mapping remains invertible. The Trunk layers can now preserve negative signals by scaling them by $\frac{1}{\alpha}$, allowing the information pipeline to remain open during the handover.
3. Numerical Instability: The "NaN" Explosion
The Identity penalty term $\lambda ||W - I||_F^2$ creates gradients proportional to the distance from identity. In the early phases of zipping, this distance is large, resulting in massive gradient magnitudes ($||\nabla|| \gg 1$). Without normalization, these updates caused the weights to overshoot, leading to floating-point overflows (NaN).
The Fixes:
- Gradient Clipping: We implemented hard clipping on the optimizer: $\nabla \leftarrow \text{clip}(\nabla, -1.0, 1.0)$. This enforces a maximum step size in the parameter space, ensuring the local linear approximation of the loss function remains valid.
- Extended Annealing: We increased the $\lambda(t)$ ramp duration from 500 to 2500 epochs . This reduced the time-derivative of the penalty ($\frac{d\mathcal{L}}{dt}$), giving the trunk network sufficient integration time to "absorb" the logic.
4. Convergence Criteria: Pareto Optimality
Our original code waited for the layer to become a perfect Identity Matrix. We found this to be impossible under Gradient Superposition. Because the $\nabla_{KD}$ (Accuracy) term always exerts some pressure, the system settles at a Pareto Optimal point where the two gradients cancel each other out.
We effectively traded "Mathematical Identity" for "Functional Identity" —a state where the matrix is diagonal enough to act as a pass-through, but noisy enough to maintain 99% accuracy.
5. Design Philosophy: Why Identity? (The "Head Switching" Fallacy)
In standard Continual Learning literature, when a researcher wants to "push" logic to a lower layer, they typically use Early Exits or Head Switching . They simply detach the classification head from Block 4 and re-attach it to Block 3.
We explicitly rejected this approach. Here is why Zipping (Identity Forcing) is fundamentally different from Head Switching , and why it is necessary for the ROGUE-Zip architecture.
A. Active Compression vs. Passive Observation
Head Switching is Passive. It asks: "Does Block 3 happen to know enough to solve the task?"
If Block 3 is only 80% accurate, moving the head accepts that 20% loss. It assumes the "intelligence" naturally resides in the upper layers and stays there.
Zipping is Active. It asks: "Can we force Block 3 to learn what Block 4 knows?"
By maintaining the connection through Block 4 while mathematically pressuring it to be an Identity Matrix, we create a back-propagation gradient that aggressively teaches Block 3. We are not just checking if the trunk is smart; we are making it smart. We are forcing the "Concept" (High-level abstraction) to be rewritten as a "Reflex" (Low-level feature).
B. The "Real Estate" Problem (Recycling vs. Abandoning)
If you simply move the Head to Block 3, Block 4 becomes dead weight. It is bypassed. It sits idle, consuming memory but contributing nothing. You have effectively made your brain smaller.
In the ROGUE-Zip protocol, the goal is not just to bypass a layer, but to recycle it.
By forcing Block 4 to become an Identity Matrix ($W \approx I$), we effectively "hollow it out."
- Current State: It acts as a wire, passing data from Block 3 to the output.
- Future State (The Goal): Because it is an Identity Matrix (linear, sparse-ish), it is the perfect starting point for Sparsity-Guided Re-training . In future phases, we can introduce new neurons into this "hollow" layer to learn Task B, while the "Identity" neurons keep passing Task A data through. You cannot easily recycle a bypassed layer; you can recycle a Zipped layer.
C. The Universal Socket
Standard neural network layers drift apart. The "language" (latent space distribution) spoken by Block 3 is usually totally different from Block 4. Moving a head requires training a brand new "Translator" (adapter).
The Identity Matrix is the Universal Socket . By forcing Block 4 to Identity, we guarantee that the output of Block 3 and the output of Block 4 exist in the same vector space . This topological alignment is critical for deep stacking. It ensures that "Down" is a consistent direction for information flow, preventing the "Covariate Shift" that usually plagues modular neural networks.
Summary: We don't just want to read the answer sooner; we want to push the computation deeper. We are turning high-level "Conscious Thoughts" (Block 4) into low-level "Instincts" (Block 3), clearing the conscious mind for the next new problem.
Risks & Future Horizons
Engaging the Skeptics & Scaling Up
The experiments in this notebook validate the physics of the "Handover Protocol," but translating ROGUE-Zip from a controlled toy experiment to a production architecture requires addressing structural risks and sketching the path to true Neuro-Symbolic hybrids.
1. What Could Go Wrong? (Risks to Scalability)
We must acknowledge that "Toy Tasks" often hide scaling laws. As we move from HCL Trainer to ImageNet or LLMs, we anticipate three specific friction points:
- The "ImageNet" Scaling Problem: In high-dimensional spaces (e.g., layer width 2048+), the Identity Penalty ($\lambda ||W - I||^2$) might be drowned out by the sheer magnitude of the accuracy gradients. We hypothesize that $\lambda$ must be normalized by layer width ($\frac{1}{\sqrt{N}}$) to maintain the tug-of-war balance.
- Batch Normalization Conflict: Standard ResNets rely on BatchNorm, which fights against fixed weight distributions. Forcing weights to $I$ may cause batch statistics to drift or explode. Future implementations may require LayerNorm or "Fixup" initializations to be Zip-compatible.
- Compute Cost: A 2500-epoch ramp is computationally expensive. We are currently investigating "One-Shot Zipping" —using Low-Rank Factorization to approximate the Identity transition instantly, potentially skipping the ramp entirely.
2. Solving Interference: The Sparse Roadmap
The failure of Experiment B (L1 $\to$ L2) was instructive. It revealed that while we can move logic, the "Trunk" can still suffer from Superposition Interference (Elhage et al., 2022) . The network used polysemantic neurons to solve L1 (Motion), leaving no orthogonal subspace for L2 (Category).
The Solution: Neural Reservations
To mitigate this, we are developing a Group Lasso protocol (Yuan & Lin, 2006).
Unlike standard weight decay, Group Lasso enforces neuron-level sparsity (forcing entire columns to zero).
- Step 1: Train the foundation with high Group Lasso, forcing the network to solve the task using only 20% of neurons.
- Step 2: When we Zip and switch tasks, the active neurons are locked, but the 80% "Dead" neurons wake up to handle the new semantic structure.
3. The Neuro-Symbolic Vision
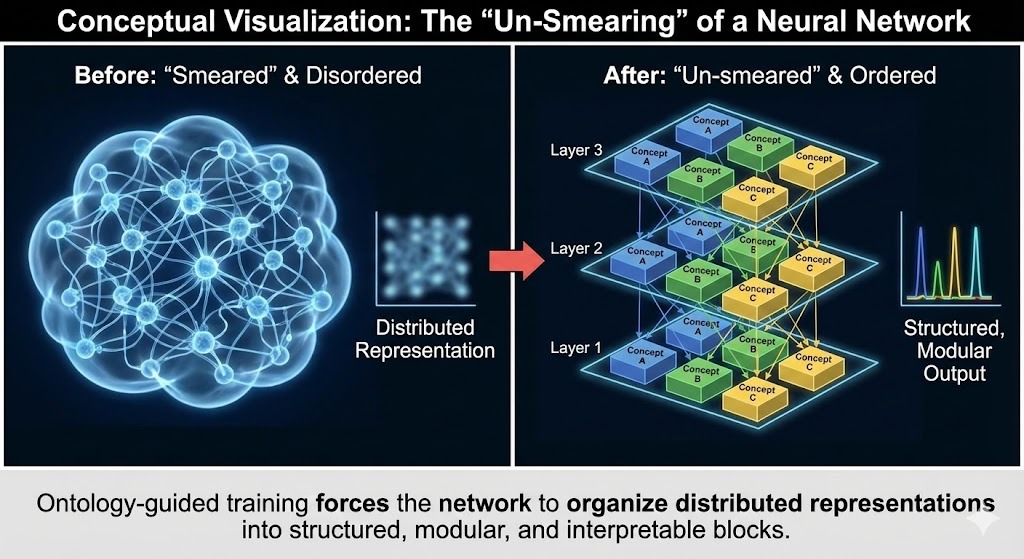
This project is not just about Continual Learning; it is a path toward "Un-Smearing" the black box.
The fundamental problem with neural networks is their holographic nature. A single concept, like "Mammal," is distributed across millions of weights. To change that concept, you must touch all those weights, inevitably disrupting everything else.
The vision of ROGUE-Zip is to force the neural network to betray its own nature. By using a strict Ontology as a curriculum, and then Zipping and locking layers one by one, we aim to coerce the network into organizing itself into discrete, modular blocks. We are trying to build a brain where "Mammal" lives in Block 3, Neurons 10-50 , and "Vehicle" lives in Block 3, Neurons 60-100 .
If successful, this architecture would transform the neural network from an opaque smear into a structured, queryable engine—combining the noise-tolerance of deep learning with the modularity and infinite extensibility of a symbol system
References
- Bengio, Y., et al. (2009). Curriculum learning. Proceedings of the 26th Annual International Conference on Machine Learning (ICML) .
- Chen, T., Goodfellow, I., & Shlens, J. (2015). Net2Net: Accelerating Learning via Knowledge Transfer. International Conference on Learning Representations (ICLR) .
- Elhage, N., et al. (2022). Toy Models of Superposition. Transformer Circuits Thread .
- McClelland, J. L., McNaughton, B. L., & O'Reilly, R. C. (1995). Why there are complementary learning systems in the hippocampus and neocortex. Psychological Review .
- McCloskey, M., & Cohen, N. J. (1989). Catastrophic interference in connectionist networks. The Psychology of Learning and Motivation .
- Yuan, M., & Lin, Y. (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B .